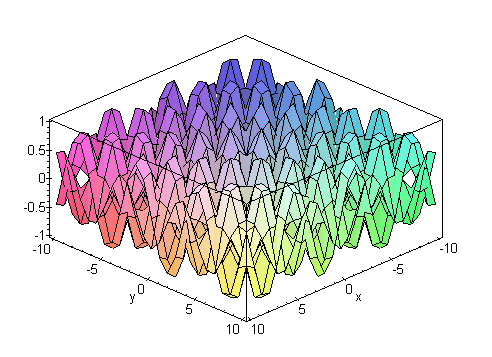
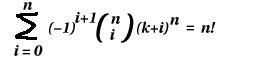This little formula does absolutely nothing (that i know of).
Actually, I do... it all started way back at Kutztown
University. I was a math major. Then I realized that computers were more my thing. One day I was
screwing around with some numbers and came upon this little formula (actually, I just found the
pattern). Four years later, Dr. Thang Bui from Penn State
Harrisburg helped me get the formula into an explainable format.
Basically, what the formula says is this:
- take an arbitrary n
- take n+1 (k) positive consecutive integers
- take those integers to the power n
- subtract the lesser from the greater going down the column, forming a new column
- this should leave you with a column containing one less element than before
- keep doing this until you get one number (a total of n columns of subtraction)
- this number is n factorial (n!)
Example:
pick n = 3, n + 1 numbers (1, 2, 3, 4)
k^3
----
| 1^3 = 1 |
| 7 |
| 2^3 = 8 | | 12 |
| 19 | | 6 |
| 3^3 = 27 | | 18 |
| 31 |
| 4^3 = 64 |
the rightmost number is 6 which is 3! (that's 3 factorial).
if you were to continue this by adding 5^3 to the leftmost column and began subtracting in
the same way, the answer after n columns of subtraction would still be 6. you can start at
1456 and the same thing would happen (1456, 1457, 1458, 1459).
this is also handy for showing that 0! = 1 (although NOT a proof!)
pick n = 0 and n + 1 arbitrary postive consecutive integers (in this case, 17,
thanks Dr. Hartzler)
k^0
----
since n = 0 and you have to do n columns of subtraction, you're already done!
so 0! = 1
Here's the equation for this bad boy:
I've written a program to replicate this and show that it works but i don't have it here
yet. It was written for Linux (which you should be
using anyway). If i recall correctly, the program works until 1178, but the segfaults get
all pissy after that. An issue i will try to resolve. And it takes a loooonnnggg time to
compute 1178 (1179^1178 is one big-ass number). So plan on this thing sitting around for a
little while. I won't be releasing the source code because it's a foul piece of shit.
Global arrays of char's flying everywhere, and i HATE commenting. If it's tough to write,
it should be tough to read.
Stay tuned for my next formula! It discovers another pattern in Pascal's Triangle...
if you read each row of pascal's triangle as one concatenated number, that number is
11^(row index base 0). so 1 = 11^0, 11 = 11^1, 121 = 11^2, and so on. BUT... it stops on
the sixth line... 1 5 10 10 5 1 (or 15101051, concatenated) is NOT 11^5! i can show you
that it IS with an algorithm i've created. This one was created AFTER i left kutztown so
don't go thinking that kutztown is some kind of a mecca for creative math people. More
later... (although flooding my mailbox will cause me to get the formula up quicker)
Any questions or comments? Email
Me
Meanwhile, here's a little something I fired up in Maple V. Bitchin':
f(x,y) = sin(x)cos(y), g(x,y) = sin(y)cos(x)